為何測試呈陽性，得病的機率還是不高?

作者：謝謝網友的提醒，得了HIV不代表有愛滋病(病發)，在原文字眼上修改了一下。

上月仁安醫院告知一孕婦陳太，其HIV(human immunodeficiency virus，人類免疫缺陷病毒，造成愛滋病的病毒)測試呈陽性，慘令花容失色，險逢家變。[1] HIV可經血液傳胎兒，因此測出愛滋對孕婦的打擊尤其大。事主事後在威爾斯醫院和內地醫院再作測試，均發現結果為陰性，始懷疑仁安醫院的測試出錯。[2] 先不論仁安的醫生說「口水都會傳染愛滋病」、「仁安當日更改化驗報告，『由陽變陰』」這些一般人也不會、不應犯的錯誤，是否屬實，仁安醫院的測試出錯，有否給我們一些教訓？總括來說，一般人對疾病測試有兩種統計學上的誤解：

1. 疾病測試是完美的。
2. 非完美但可靠的疾病測試中，陽性代表患病的機會很高。


測試呈陽性不等於有病

這個概念的確違反常識。常識是，疾病測試就是要找出是否有病，陽性(positive)就是有病，陰性(negative)就是無。我們信任現代醫學，所以平時對測試結果沒有懷疑，這也是陳太為何因測試報告大受打擊的原因。

但我們也知道測試有可能出錯，也就是說：陽性不等於有病，陰性也不等於無病。反過來說，有病也不一定呈陽性，而無病也不一定呈陰性。無病而呈陽性，稱為「假陽性(false positive)」；有病而呈陰性，稱為「假陰性(false negative)」。

HIV測試系統不是完美的(其實沒有系統是完美的)，它可以因為污染、資料錯誤、機器錯誤而造成假陽性假陰性，而測試本身因為是基於抗體和抗原蛋白的結合，本身也潛在其他非HIV抗體的結合，所以也可造成假陽性。[3] 當然醫學界應該，也已致力盡量把這些可能性降到十分低的水平。威院稱愛滋測試有0.1%假陽性率(false positive rate)。也就是說每1000個無HIV的人的測試中，平均會有1人呈陽性。[1] (留意這和「每1000個陽性結果中有1個錯」是不一樣的。)

愛滋測試呈陽性不是世界末日

好，你已經接受了HIV測試不完美這個事實了嗎？接著要告訴你，即使測試十分可靠(假陽性率很低)，陽性也*不*代表感染HIV的機會很高。簡言之，這是因為有HIV的人的比例本來就很低。根據某些研究，HIV測試的假陰性率為0.3%(0.003)。[4] 衛生署公佈2015年的HIV感染個案為7718 [6]，而香港人口為7,324,300，即HIV感染率為7718/ 7324300 = 0.105% (0.00105)。[7]

那麼如果HIV測試呈陽性，有該病毒的機會有多大？我們將會看見，這和「如有HIV，測試呈陽性」的機會是兩個完全不同的概念，而即使假陽性率極低，如陽性有HIV的機會也不一定大。


以貝葉斯概率(Bayesian probability)計算(可跳過計算，到圖表解說)：

設P為HIV測試呈陽性的事件，D為有HIV的事件。如陽性有HIV的或然率為
Pr (D | P) = Pr (D & P) / Pr (P) -------------- Eq. 1
有HIV也是陽性的機會Pr (D & P)和陽性的機會Pr (P) 不能直接得知，需要計算。

計算Pr (D & P):
Pr (D & P) = Pr (P | D) Pr (D)
如有HIV，陰性的機會(假陰性率) Pr (not P | D) = 0.003
那麼如有HIV，陽性的機會Pr (P | D) = 1 – 0.003 = 0.997
有HIV的機會Pr (D) = 0.00105
Pr (D & P) = Pr (P & D) = Pr (P | D) Pr (D)
= 0.997 x 0.00105 = 0.00104685

計算Pr (P):
測試呈陽性只有兩個可能性：有HIV和無HIV
Pr (P) = Pr (P & D) + Pr (P & not D)
Pr (P & D) 已計算
Pr (P & not D) = Pr (P | not D) Pr (not D)
根據威院，如無HIV，陽性的機會(假陽性率) Pr (P | not D) = 0.001
無HIV的機會 Pr (not D) = 1 – 0.00105 = 0.99895
Pr (P & not D) = 0.001 x 0.99895 = 0.00099895
Pr (P) = 0.00104685 + 0.000998946 = 0.0020458

回到Eq. 1，Pr (D | P) = Pr (D & P) / Pr (P)
= 0.00104685 / 0.0020458 = 51.2%

也就是說，即使HIV測試呈陽性，閣下真正得了HIV的機會也只有約一半。這是因為香港的HIV感染率(0.105%)相對全球的感染率(0.8%)低很多，愛滋病在香港是罕有的病。[5]


以圖表解說

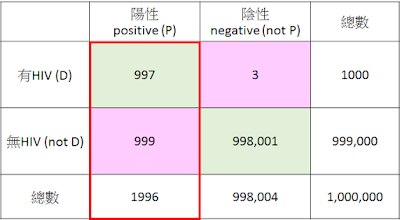
為了簡化圖表，假設一城市內有一百萬人，HIV感染率(0.1%)，假陽性率(0.1%)和假陰性率(0.3%)都和香港相若。如此，城內有1,000,000 x 0.001 = 1000人感染HIV。

如果全城去驗HIV，假陽性有999,000 x 0.001 = 999宗，假陰性有1000 x 0.003 = 3宗。

那麼，如果HIV測試呈陽性，有該病毒的機會 = 997/ 1996 = 49.9%，約是一半。見下圖紅框內部份。

正確面對陽性的疾病測試結果

根據以上的教訓，那麼，作為醫生和病人，該如何面對陽性的測試結果？首先，所有醫生都要對統計學有正確的認識，同時也要適當地對病人傳達有關不確定性和風險(uncertainty and risk)的信息，讓病人基於現有的資訊上作出正確的治療決定。病人也應了解沒有測試是完美的，冷靜地消化測試結果，遇上罕有疾病的陽性測試結果，必需要覆檢以確定是否患病，以決定是否進一步接受檢查和治療。固然，醫療失誤茲事體大，要嚴肅處理，但我們每一個人，都應多多少少對於疾病測試和統計學有些正確的認識，這也正是大眾科學和數學教育之所以重要的其中一個原因。

延伸閱讀：Gigerenzer, G. (2002). Calculated risks: How to know when numbers deceive you. New York: Simon & Schuster. ISBN-10: 0-74320-556-1 ISBN-13: 978-0-74320-556-6


參考:

[1] 仁安驗錯當愛滋 孕婦蒙冤 - Yahoo 新聞香港
https://hk.news.yahoo.com/%E4%BB%81%E5%AE%89%E9%A9%97%E9%8C%AF%E7%95%B6%E6%84%9B%E6%BB%8B-%E5%AD%95%E5%A9%A6%E8%92%99%E5%86%A4-220028553.html

[2] 都市日報 - 仁安疑錯判孕婦患愛滋
http://www.metrohk.com.hk/index.php?cmd=detail&id=308831

[3] HIV & AIDS - Factors Known to Cause False Positive HIV Antibody Test Results
http://www.virusmyth.com/aids/hiv/cjtestfp.htm

[4] Diagnosis of HIV/AIDS - Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Diagnosis_of_HIV/AIDS#Accuracy_of_HIV_testing

[5] WHO | HIV/AIDS
http://www.who.int/gho/hiv/en/

[6] 愛滋病網上辦公室 最新公佈數字一覽表
http://www.info.gov.hk/aids/chinese/surveillance/quarter.htm

[7] 人口 - 概述 | 政府統計處
http://www.censtatd.gov.hk/hkstat/sub/so20_tc.jsp